Description of Reactor Fuel Breeding with Three Integral Concepts

The time-dependent breeding of fuel in a growing system of breeder reactors can be characterized by the transitory (instantaneous) growth rate, γ(t), which expresses both fuel and reactor properties. The three most important aspects of γ(t) can be expressed by time-independent integral concepts. Two of these concepts are in widespread use, although they are not generally calculated from the same definitions. A third integral concept that links the two earlier ones is introduced here. The time-dependent growth rate has an asymptotic value, γ^∞, the equilibrium growth rate, which is the basis for the calculation of the doubling time. The equilibrium growth rate measures the breeding capability and represents a reactor property. Maximum deviation of γ(t) and γ^∞ generally appears at the initial startup of the reactor, where γ(t = 0) = γ₀. This deviation is due to the difference between the initial and asymptotic fuel inventory composition. The initial growth rate can be considered a second integral concept; it characterizes the breeding of a particular fuel in a given reactor. Growth rates are logarithmic derivatives of the growing mass of fuel in breeder reactors, especially γ^∞, which describes the asymptotic growth by exp(γ^∞t). There is, however, a variation in the fuel-mass factor in front of this exponential function during the transition from γ₀ to γ^∞. It is shown here that this variation of the fuel mass during transition can be described by a third integral concept, termed the breeding bonus, b. The breeding bonus measures the quality of a fuel for its use in a given reactor in terms of its impact on the magnitude of the asymptotically growing fuel mass. It is therefore an integral concept that comprises both fuel and reactor properties. Integral breeding concepts are generally calculated by application of a set of weight factors to the respective isotopic reaction rate and inventory components. So, the calculation of γ₀ and γ^∞ is facilitated by use of the critical mass (CM) worths (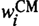) and the breeding worth factors (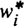), respectively. It is shown here that the calculation of the breeding bonus, as a quantity that links initial and asymptotic fuel growth, is based on the joint application of 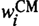and 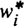.